Möbius Transformations For Global Intrinsic Symmetry Analysis
Computer Graphics Forum (Symposium on Geometry Processing), July 2010
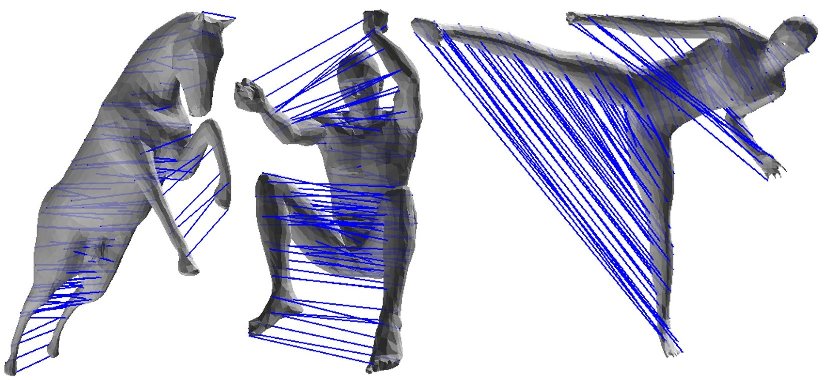
Intrinsically symmetric point correspondences
Abstract
The goal of our work is to develop an algorithm for automatic and robust detection of global intrinsic symmetries
in 3D surface meshes. Our approach is based on two core observations. First, symmetry invariant point sets can
be detected robustly using critical points of the Average Geodesic Distance (AGD) function. Second, intrinsic
symmetries are self-isometries of surfaces and as such are contained in the low dimensional group of Möbius
transformations. Based on these observations, we propose an algorithm that: 1) generates a set of symmetric points
by detecting critical points of the AGD function, 2) enumerates small subsets of those feature points to generate
candidate Möbius transformations,and 3) selects among those candidate Möbius transformations the one(s) that
best map the surface onto itself. The main advantages of this algorithm stem from the stability of the AGD in
predicting potential symmetric point features and the low dimensionality of the Möbius group for enumerating
potential self-mappings. During experiments with a benchmark set of meshes augmented with human-specified
symmetric correspondences, we find that the algorithm is able to find intrinsic symmetries for a wide variety of
object types with moderate deviations from perfect symmetry.
Links
Citation
Vladimir Kim, Yaron Lipman, Xiaobai Chen, and Thomas Funkhouser.
"Möbius Transformations For Global Intrinsic Symmetry Analysis."
Computer Graphics Forum (Symposium on Geometry Processing) 29(5), July 2010.
BibTeX
@article{Kim:2010:MTF,
author = "Vladimir Kim and Yaron Lipman and Xiaobai Chen and Thomas Funkhouser",
title = "M{\"o}bius Transformations For Global Intrinsic Symmetry Analysis",
journal = "Computer Graphics Forum (Symposium on Geometry Processing)",
year = "2010",
month = jul,
volume = "29",
number = "5"
}