Interior Distance Using Barycentric Coordinates
Computer Graphics Forum (Symposium on Geometry Processing), July 2009
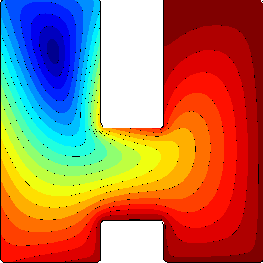
The interior distance measured from a single source point (small distances are blue, large ones are red) inside a 2D shape.
Abstract
This paper introduces a framework for defining a shape-aware
distance measure between any two points in the interior of a surface mesh.
Our framework is based on embedding the surface mesh into a
high-dimensional space in a way that best preserves boundary
distances between vertices of the mesh, performing a mapping of the
mesh volume into this high-dimensional space using barycentric
coordinates, and defining the interior distance between any two
points simply as their Euclidean distance in the embedding space. We
investigate the theoretical properties of the interior distance in
relation to properties of the chosen boundary distances and
barycentric coordinates, and we investigate empirical properties of
the interior distance using diffusion distance as the prescribed
boundary distance and mean value coordinates. We prove
theoretically that the interior distance is a metric, smooth,
interpolating the boundary distances, and reproducing Euclidean
distances, and we show empirically that it is insensitive to
boundary noise and deformation and quick to compute. In case the barycentric coordinates
are non-negative we also show a maximum principle exists. Finally,
we use it to define a new geometric property, barycentroid of shape,
and show that it captures the notion of semantic center of the
shape.
PDF File
- Paper (PDF)
Citation
Raif Rustamov, Yaron Lipman, and Thomas Funkhouser.
"Interior Distance Using Barycentric Coordinates."
Computer Graphics Forum (Symposium on Geometry Processing) 28(5), July 2009.
BibTeX
@article{Rustamov:2009:IDU,
author = "Raif Rustamov and Yaron Lipman and Thomas Funkhouser",
title = "Interior Distance Using Barycentric Coordinates",
journal = "Computer Graphics Forum (Symposium on Geometry Processing)",
year = "2009",
month = jul,
volume = "28",
number = "5"
}