Symmetry Factored Embedding and Distance
ACM Transactions on Graphics (SIGGRAPH 2010), July 2010
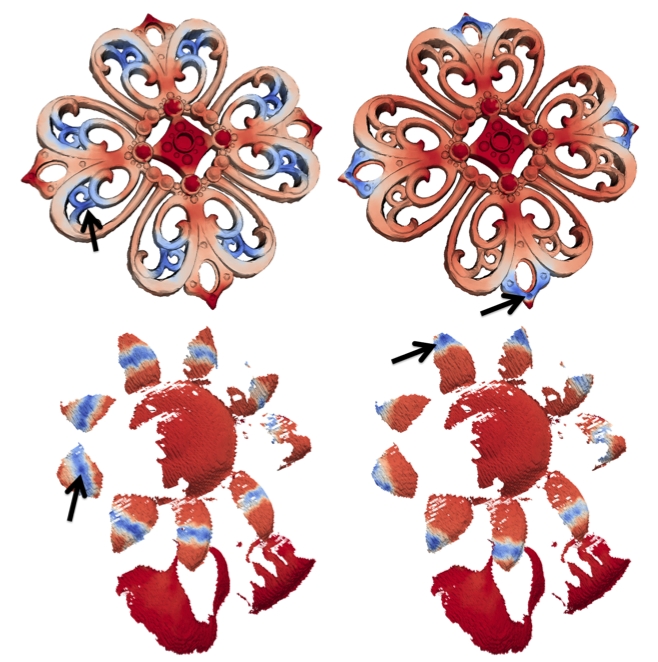
Symmetry Factored Distance measured from the points marked by black arrows (blue is small distance, red is large).
Abstract
We introduce the Symmetry Factored Embedding (SFE) and the
Symmetry Factored Distance (SFD) as new tools to analyze and
represent symmetries in a point set. The SFE provides new coordinates
in which symmetry is “factored out,” and the SFD is the Euclidean
distance in that space. These constructions characterize the
space of symmetric correspondences between points – i.e., orbits.
A key observation is that a set of points in the same orbit appears
as a clique in a correspondence graph induced by pairwise similarities.
As a result, the problem of finding approximate and partial
symmetries in a point set reduces to the problem of measuring
connectedness in the correspondence graph, a well-studied problem
for which spectral methods provide a robust solution. We provide
methods for computing the SFE and SFD for extrinsic global symmetries
and then extend them to consider partial extrinsic and intrinsic
cases. During experiments with difficult examples, we find that
the proposed methods can characterize symmetries in inputs with
noise, missing data, non-rigid deformations, and complex symmetries,
without a priori knowledge of the symmetry group. As such,
we believe that it provides a useful tool for automatic shape analysis
in applications such as segmentation and stationary point detection.
Links
- Paper (pdf)
Citation
Yaron Lipman, Xiaobai Chen, Ingrid Daubechies, and Thomas Funkhouser.
"Symmetry Factored Embedding and Distance."
ACM Transactions on Graphics (SIGGRAPH 2010), July 2010.
BibTeX
@article{Lipman:2010:SFE,
author = "Yaron Lipman and Xiaobai Chen and Ingrid Daubechies and Thomas
Funkhouser",
title = "Symmetry Factored Embedding and Distance",
journal = "ACM Transactions on Graphics (SIGGRAPH 2010)",
year = "2010",
month = jul
}